Analisis spasial merupakan pendekatan statistik yang mempertimbangkan lokasi geografis sebagai faktor penting dalam melihat distribusi data. Salah satu metode yang umum digunakan untuk mendeteksi pola spasial adalah Moran’s I untuk autokorelasi global, dan LISA (Local Indicators of Spatial Association) untuk autokorelasi lokal.
Dalam analisi ini, dilakukan analisis spasial terhadap data jumlah murid Sekolah Dasar di Provinsi Bali selama periode 2019-2023, untuk mengidentifikasi potensi klaster spasial konsentrasi siswa tinggi maupun rendah. Data yang digunakan meliputi:
- Data spasial: Shapefile batas administrasi kabupaten di Provinsi Bali.
- Data atribut: Jumlah murid Sekolah Dasar per tahun di tiap kabupaten selama lima tahun terakhir (2019-2023) dari BPS.
Rumus Moran's I
Moran's I adalah ukuran autokorelasi spasial global yang digunakan untuk mengevaluasi sejauh mana suatu variabel bersifat mengelompok secara spasial. Rumus lengkap dari Moran’s I adalah sebagai berikut:

Dimana:
- 𝐼 : Statistik Moran’s I
- 𝑛 : Jumlah unit spasial (misalnya kabupaten/kota)
- 𝑥𝑖 : Nilai variabel di lokasi ke- 𝑖
- 𝑥¯ : Rata-rata dari variabel 𝑥
- 𝑤𝑖𝑗 : Elemen dari matriks bobot spasial 𝑊 yang menunjukkan hubungan spasial antara lokasi 𝑖 dan 𝑗
- 𝑊 : Jumlah total dari semua bobot spasial, yaitu ∑𝑖∑𝑗𝑤𝑖𝑗
Interpretasi Nilai Moran’s I
- 𝐼>0 → Terdapat autokorelasi spasial positif (klaster mirip berdampingan)
- 𝐼<0 → Terdapat autokorelasi spasial negatif (wilayah berbeda berdampingan)
- 𝐼≈0 → Tidak ada pola spasial (acak)
Uji signifikansi dapat dilakukan melalui simulasi randomisasi atau z-score standar deviasi.

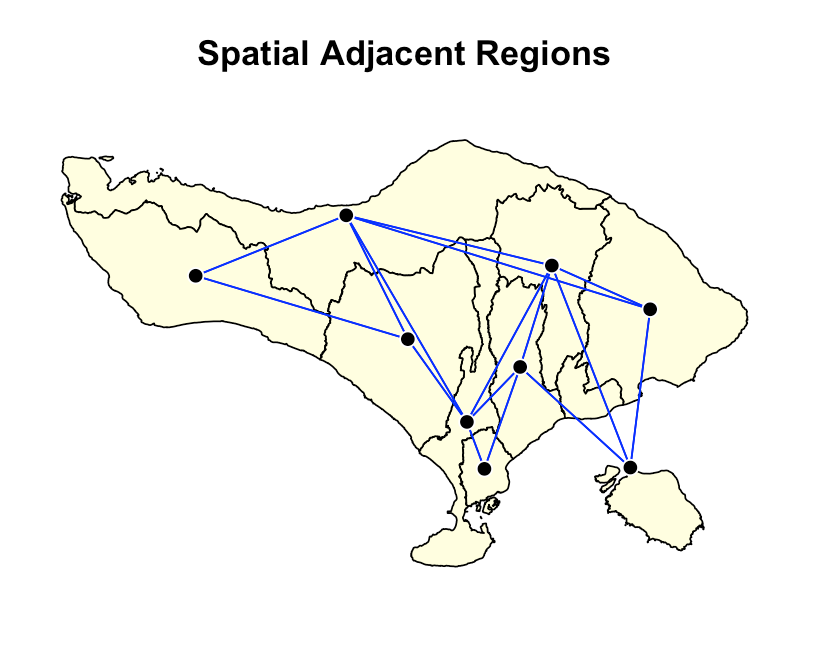
* Titik pusat (centroid) untuk kabupaten Klungkung pada peta bukan tidak tepat, namun hal ini dikarenakan di Nusa Penida, Nusa Lembongan, dan Nusa Ceningan masih ada yang termasuk kabupaten Klungkung (beda pulau), maka titiknya menjadi ambigu.


MORANS I
Uji Moran I yang dilakukan pada dataset jumlah murid Sekolah Dasar di Provinsi Bali dari tahun 2019 hingga 2023 bertujuan untuk menguji adanya autokorelasi spasial, yaitu apakah nilai-nilai suatu variabel di suatu lokasi cenderung berkorelasi dengan nilai di lokasi-lokasi yang berdekatan. Hasil dari uji ini memberikan gambaran apakah terdapat pola spasial yang signifikan dalam data, yang bisa berupa pengelompokan (clustering) atau pemisahan (dispersion) nilai-nilai tertentu berdasarkan lokasi geografis.
Dalam setiap uji Moran’s I pada dataset dari tahun 2019 hingga 2023, diperoleh p-value yang lebih besar dari 0.05. Ini berarti bahwa tidak ada bukti statistik yang cukup untuk menolak hipotesis nol, yang menyatakan bahwa tidak ada autokorelasi spasial yang signifikan dalam data. Dengan kata lain, jumlah murid Sekolah Dasar di kabupaten-kabupaten di Bali tidak menunjukkan pola spasial yang terstruktur atau hubungan spasial yang signifikan antara lokasi-lokasi yang berdekatan.
Pada data tahun 2019, nilai statistik Moran’s I adalah 0.0349, dengan p-value 0.2097, yang menunjukkan bahwa tidak ada pengelompokan atau pemisahan yang signifikan.
Menariknya, pada tahun 2021, nilai Moran’s I menjadi sedikit negatif (-0.0036), namun dengan p-value 0.2715 tetap menunjukkan tidak adanya autokorelasi spasial yang signifikan.
Demikian pula, pada tahun 2020, 2022 dan 2023, meskipun nilai statistik Moran’s I bervariasi sedikit antar tahun, p-value yang secara konsisten lebih besar dari 0.05 mengindikasikan bahwa distribusi jumlah murid Sekolah Dasar di Provinsi Bali cenderung acak secara spasial, tanpa adanya kecenderungan bahwa kabupaten-kabupaten dengan jumlah murid tinggi atau rendah mengelompok secara geografis.


Analisis Local Moran (LISA)

Integrated Nested Laplace Approximation (INLA)
Integrated Nested Laplace Approximation (INLA) adalah metode komputasi yang digunakan untuk menghitung distribusi posterior dalam model Bayesian. INLA digunakan terutama untuk model statistik yang melibatkan parameter dan data dengan ketergantungan spasial dan temporal. INLA menawarkan alternatif yang lebih efisien dibandingkan dengan pendekatan Markov Chain Monte Carlo (MCMC), dengan menghitung distribusi posterior melalui pendekatan deterministik, sehingga lebih cepat dalam aplikasi pemodelan yang besar.
INLA pertama kali diperkenalkan oleh Rue et al. (2009) untuk menyelesaikan masalah komputasi yang kompleks dalam pemodelan Bayesian dengan data spasial dan temporal.
INLA adalah metode yang sangat efisien untuk pemodelan Bayesian, khususnya dalam analisis data spasial dan temporal. Dengan keuntungan utama berupa kecepatan komputasi yang lebih tinggi dibandingkan dengan metode MCMC, INLA memungkinkan estimasi parameter model yang akurat tanpa membutuhkan simulasi acak besar.

Model ini menggunakan pendekatan Bayesian melalui metode INLA (Integrated Nested Laplace Approximation), dengan struktur model gabungan antara efek spasial (BYM2) dan efek temporal (RW1).
Computational cost :
Pre: Waktu untuk mempersiapkan struktur model dan data.
Running: Waktu yang dibutuhkan INLA untuk melakukan perhitungan numerik (approximate Bayesian inference).
Post: Waktu pasca perhitungan untuk merangkum hasil.
Total: Waktu keseluruhan proses pemodelan.
Total waktu komputasi: 5.18 detik, ini menunjukkan efisiensi metode INLA dibanding metode sampling seperti MCMC.
Fixed Effect (Efek Tetap)
(Intercept): mean = 45627.73, sd = 0.039, CI95% = [45627.73, 45627.81]
Intercept menunjukkan nilai rata-rata jumlah murid SD di Bali ketika seluruh efek acak (spasial & temporal) bernilai nol. Karena rentang interval kepercayaannya sangat kecil, hasil estimasi ini bisa dianggap sangat akurat dan tidak banyak mengandung ketidakpastian.
Efek Acak (Random Effects)
1. Efek Spasial Efek spasial dimodelkan menggunakan pendekatan BYM2, yaitu gabungan dari dua komponen:
- Structured effect: Menggambarkan pengaruh spasial terstruktur berdasarkan kedekatan geografis antar kabupaten (informasi tetangga).
- Unstructured effect: Menggambarkan variasi lokal yang bersifat acak dan tidak berkaitan dengan kedekatan spasial (noise).
2. Efek Temporal Efek waktu dimodelkan menggunakan Random Walk of Order 1 (RW1), dengan asumsi bahwa perubahan jumlah murid terjadi secara bertahap dan halus antar tahun, di mana nilai pada suatu tahun bergantung pada nilai tahun sebelumnya.
Interpretasi Parameter Model INLA (Spasio-Temporal)
Dalam model spasio-temporal yang dibangun menggunakan pendekatan Bayesian INLA, terdapat beberapa parameter penting yang menggambarkan ketepatan (precision) dan kontribusi masing-masing komponen model, baik residual, spasial, maupun temporal. Berikut interpretasinya berdasarkan hasil output:
Precision for the Gaussian Observations –> 62.188
Parameter ini menunjukkan ketepatan (precision) dari error residual model. Semakin tinggi precision, maka varians error semakin kecil. Nilai 62.188 menunjukkan bahwa prediksi model cukup presisi, dengan tingkat kesalahan residual yang rendah.
Precision untuk Efek Spasial (id_kab) –> 88.719
Ini adalah precision untuk efek spasial antar kabupaten dengan model BYM2 (Besag-York-Mollié 2). Nilai precision sebesar 88.719 menunjukkan bahwa variasi antar kabupaten cukup stabil dan tidak terlalu dipengaruhi oleh fluktuasi acak besar, mencerminkan keyakinan tinggi terhadap pola spasial yang ada.
Phi untuk Efek Spasial (id_kab) –> 0.087
Phi mengukur proporsi variasi spasial yang berasal dari struktur spasial terstruktur (structured spatial effect). Nilai 0.087 berarti hanya sekitar 8.7% variasi spasial berasal dari struktur spasial antar wilayah (misalnya kabupaten yang bertetangga), sementara sisanya (91.3%) berasal dari variasi spasial yang tidak terstruktur (random noise atau efek lokal spesifik).
Artinya, sebagian besar perbedaan jumlah murid antar kabupaten disebabkan oleh faktor lokal yang tidak berkaitan langsung dengan hubungan geografis.
Precision untuk Efek Temporal (time, RW1) –> 51.253
Efek temporal dimodelkan menggunakan Random Walk 1 (RW1), yang mengasumsikan perubahan halus dari tahun ke tahun. Nilai precision sebesar 51.253 menunjukkan bahwa perubahan antar tahun bersifat cukup stabil dan tidak mengalami fluktuasi besar. Ini sesuai dengan asumsi bahwa tren waktu jumlah murid bergerak perlahan dan tidak ekstrem.

Efek temporal adalah bagian dari model spasio-temporal yang merepresentasikan dinamika atau variasi suatu fenomena seiring waktu. Dalam konteks pemodelan INLA, efek temporal biasanya dimodelkan menggunakan Random Walk (RW) , yang paling umum adalah RW1 dan RW2.
Model RW1 (Random Walk of order 1) mengasumsikan bahwa nilai pada waktu ke-𝑡 bergantung pada nilai di waktu sebelumnya, yaitu:

Dimana:
- 𝜃𝑡 = efek acak pada waktu 𝑡
- 𝜏 = presisi (kebalikan dari varians)
- 𝜖𝑡 = gangguan acak Gaussian
RW1 sering digunakan ketika asumsi bahwa perubahan antarwaktu bersifat linier dan halus dianggap masuk akal.

Kesimpulan
1. Tidak Terdapat Autokorelasi Spasial Global yang Signifikan
Hasil uji Moran’s I dari tahun ke tahun menghasilkan nilai yang mendekati nol dan p-value > 0.05, yang menunjukkan tidak adanya pola spasial global yang signifikan. Artinya, distribusi jumlah murid di kabupaten/kota di Bali cenderung acak secara spasial dan tidak membentuk pola klaster besar antar wilayah.
2. Deteksi Pola Lokal Konsisten Melalui LISA
Meskipun tidak signifikan secara global, peta LISA mengungkapkan pola spasial lokal yang relatif konsisten selama lima tahun. Kota Denpasar secara konsisten muncul sebagai klaster High-High, menunjukkan konsentrasi tinggi jumlah murid yang berdekatan dengan kabupaten dengan nilai tinggi lainnya, seperti Badung. Sebaliknya, Klungkung dan Karangasem sering muncul sebagai Low-Low, mengindikasikan klaster konsentrasi rendah.
3. Variasi Jumlah Murid Lebih Dipengaruhi Faktor Lokal
Model spasial BYM2 menunjukkan nilai Phi sebesar 0.087, artinya hanya sekitar 8.7% variasi spasial yang berasal dari struktur spasial (kedekatan geografis), sementara sisanya berasal dari variasi lokal yang tidak terstruktur. Ini memperkuat temuan bahwa faktor-faktor lokal di masing-masing kabupaten lebih dominan daripada pengaruh geografis antar wilayah.
4. Tren Temporal Stabil dan Konsisten
Efek waktu berdasarkan model RW1 menunjukkan penurunan efek temporal dari tahun 2019 hingga 2022, dengan sedikit peningkatan pada 2023. Ini mengindikasikan adanya penurunan jumlah murid SD secara umum selama pandemi, diikuti sedikit pemulihan. Nilai precision RW1 sebesar 51.253 menegaskan bahwa perubahan antar tahun bersifat halus dan tidak ekstrem.
5. Efektivitas Metode INLA
Metode INLA terbukti efisien untuk analisis spasio-temporal. Dengan waktu komputasi hanya sekitar 5 detik dan estimasi parameter yang stabil, INLA mampu menangkap kontribusi spasial dan temporal secara simultan serta memberikan gambaran posterior yang akurat.
Rekomendasi
Pendekatan kebijakan berbasis lokal
Perlu diperkuat karena ketimpangan jumlah murid lebih bersumber dari karakteristik spesifik masing-masing kabupaten.
Pemetaan LISA dapat dimanfaatkan untuk prioritas alokasi
Sumber daya pendidikan, seperti dukungan tambahan bagi daerah dengan klaster Low-Low.
Pemantauan temporal
Harus terus dilakukan pasca-pandemi untuk memastikan tren peningkatan jumlah murid benar-benar berlanjut.


![[GEODATA] Tutupan Lahan Indonesia](https://mapidstorage.s3.amazonaws.com/general_image/mapidseeit/1684312961161_COVER%20GEODATA_%20Tutupan%20Lahan.png)
![[GEODATA] Status Ekonomi dan Sosial (SES) Indonesia](https://mapidstorage.s3.amazonaws.com/general_image/mapidseeit/1693454652933_20230831-085941.jpg.jpeg)